A Tipler Cylinder uses a massive and long
cylinder spinning around its longitudinal axis. The rotation
creates a frame-dragging effect and fields of closed time-like
curves traversable in a way to achieve subluminal time travel to
the past.
Civilizations with the technology to harness black holes might
be better advised to leave wormholes alone and try the time-warp
method suggested by U.S. astronomer Frank Tipler. He has a
simple recipe for a time machine: First take a piece of material
10 time the mass of the Sun, squeeze it together and roll it
into a long, thin, super-dense cylinder – a bit like a black
hole that has passed through a spaghetti factory. Then spin the
cylinder up to a few billion revolutions per minute and see what
happens.
Tipler predicts that a ship following a carefully plotted spiral
course around the cylinder would immediately find itself on a
"closed, time-like curve." It would emerge thousands, even
billions, of years from its starting point and possibly several
galaxies away. There are problems, though. For the mathematics
to work properly, Tipler’s cylinder has to be infinitely long.
Also, odd things happen near the ends and you need to steer well
clear of them in your timeship. However, if you make the device
as long as you can, and stick to paths close to the middle of
the cylinder, you should survive the trip!

The Tipler cylinder, also called a Tipler time machine, is a
hypothetical object theorized to be a potential mode of time
travel—an approach that is conceivably functional within
humanity's current understanding of physics, specifically the
theory of general relativity, although later results have shown
that a Tipler cylinder could only allow time travel if its
length would appear infinite.
The key characteristics of the application of Tipler Cylinders
for time control and time travel are presented in the picture
below. This is followed by more detail describing the approach
below.

The Tipler cylinder was discovered as a solution to the
equations of general relativity by Willem Jacob van Stockum in
1936 and Kornel Lanczos in 1924, but not recognized as allowing
closed timelike curves until an analysis by Frank Tipler in
1974. Tipler showed in his 1974 paper, "Rotating Cylinders and
the Possibility of Global Causality Violation" that in a
spacetime containing a massive, infinitely long cylinder which
was spinning along its longitudinal axis, the cylinder should
create a frame-dragging effect. This frame-dragging effect warps
spacetime in such a way that the light cones of objects in the
cylinder's proximity become tilted, so that part of the light
cone then points backwards along the time axis on a space time
diagram. Therefore a spacecraft accelerating sufficiently in the
appropriate direction can travel backwards through time along a
closed timelike curve or CTC.
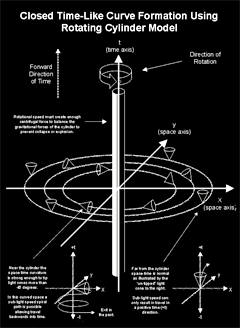
Closed timelike curve formation
using rotating cylinder model |
CTC's are associated, in Lorentzian manifolds which are
interpreted physically as spacetimes, with the possibility of
causal anomalies such as going back in time and potentially
shooting your own grandfather, although paradoxes might be
avoided using some constraint such as the Novikov
self-consistency principle. They have an unnerving habit of
appearing in some of the most important exact solutions in
general relativity, including the Kerr vacuum (which models a
rotating black hole) and the van Stockum dust (which models a
cylindrically symmetrical configuration of rotating pressureless
fluid or dust).
An objection to the practicality of building a Tipler cylinder
was discovered by Stephen Hawking, who posited a conjecture
showing that according to general relativity it is impossible to
build a time machine in any finite region that satisfies the
weak energy condition, meaning that the region contains no
exotic matter with negative energy.
The Tipler cylinder, on the other hand, does not involve any
negative energy. Tipler's original solution involved a cylinder
of infinite length, which is easier to analyze mathematically,
and although Tipler suggested that a finite cylinder might
produce closed timelike curves if the rotation rate were fast
enough, he did not prove this.
But Hawking argues that because
of his conjecture, "it can't be done with positive energy
density everywhere! I can prove that to build a finite time
machine, you need negative energy." Hawking's proof appears in
his 1992 paper on the chronology protection conjecture, where he
examines "the case that the causality violations appear in a
finite region of spacetime without curvature singularities" and
proves that "there will be a Cauchy horizon that is compactly
generated and that in general contains one or more closed null
geodesics which will be incomplete. One can define geometrical
quantities that measure the Lorentz boost and area increase on
going round these closed null geodesics. If the causality
violation developed from a noncompact initial surface, the
averaged weak energy condition must be violated on the Cauchy
horizon."
|
|
|
